Mathématiques

Mathematics for Engineers

Description: In this course, students are expected to acquire and master the formalisms, concepts, and mathematical results used in modeling physical systems or phenomena and engineering sciences. This particularly includes an advanced level in linear algebra and a thorough understanding of measure theory, Lebesgue integration, Fourier transform, and differential calculus.

Learning outcomes: By the end of this course, students will master the formalisms, concepts, and mathematical results used in modeling physical systems or phenomena and engineering sciences. They will have an advanced level in linear algebra and a thorough knowledge of measure theory, Lebesgue integration, Fourier transform, and differential calculus.

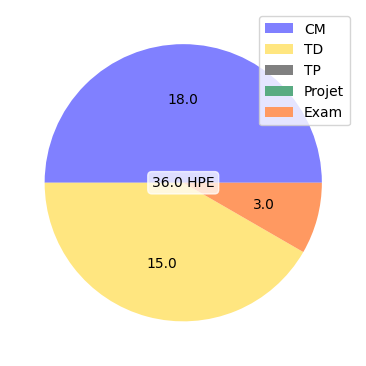
Evaluation methods: 3h written test, can be retaken.

Course supervisor: Michel Barret

Geode ID: SPM-MAT-001

CM:

1. Théorie de la mesure, intégrale de Lebesgue 1/2 (1.5 h)
2. Théorie de la mesure, intégrale de Lebesgue 2/2 (1.5 h)
3. Mesures sur des espaces produits (1/2) (1.5 h)
4. Mesures sur des espaces produits (2/2) (1.5 h)
5. Espaces vectoriels normés 1/2 (1.5 h)
6. Espaces vectoriels normés 2/2 (1.5 h)
7. Transformation de Fourier 1/2 (1.5 h)
8. Transformation de Fourier 2/2 (1.5 h)
9. Rappels et compléments d’algèbre linéaire 1/2 (1.5 h)
10. Rappels et compléments d’algèbre linéaire 2/2 (1.5 h)
11. Calcul différentiel 1/2 (1.5 h)
12. Calcul différentiel 2/2 (1.5 h)

TD:

1. Théorie de la mesure, intégrale de Lebesgue 1/2 (1.5 h)
2. Théorie de la mesure, intégrale de Lebesgue 2/2 (1.5 h)
3. Mesures sur des espaces produits (1/2) (1.5 h)
4. Mesures sur des espaces produits (2/2) (1.5 h)
5. Espaces vectoriels normés (1.5 h)
6. Transformation de Fourier 1/2 (1.5 h)
7. Transformation de Fourier 2/2 (1.5 h)
8. Rappels et compléments d’algèbre linéaire 1/2 (1.5 h)
9. Rappels et compléments d’algèbre linéaire 2/2 (1.5 h)
10. Calcul différentiel (1.5 h)