ModStat2
Statistical models 2
Description: This course is an extension of the ModStat1 course. It is structured around the three fundamental concepts of stochastic processes, latent variables and approximate inference techniques. The first part of the course on processes focuses on three main families of processes: point processes, Markov processes and Gaussian processes. The notion of latent variable is then addressed through mixture models and the EM algorithm. The two notions are then combined to develop hidden Markov models, for both discrete (HMM) and continuous states (Kalman filters). Finally, approximate inference techniques are presented, with sampling techniques (MCMC) and variational inference.
Prerequisites:
- Having followed the course “Statistical Models 1”
- Beginner level in Python / Numpy programming
Learning outcomes: At the end of this course, students will be able to associate the corresponding type of stochastic process with data series and apply the associated estimation methods. They will also be able to specify a model incorporating hidden variables and apply the EM algorithm to estimate its parameters. They will be able to model a clustering problem in the form of a mixture model. They will be able to specify an HMM or a Kalman filter to model the dynamic behavior of a discrete or continuous state system.
Evaluation methods: 3h written test with documents, can be retaken.
Evaluated skills:
- Modelling
- Research and Development
Course supervisor: Frédéric Pennerath
Geode ID: 3MD4050
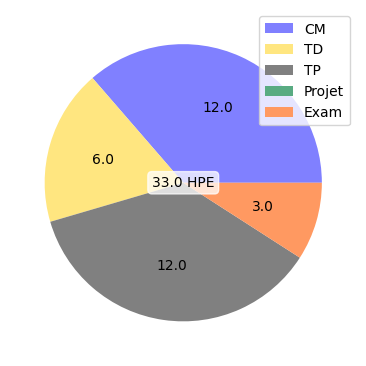
CM:
- Processus ponctuels (1.5 h)
- Processus de Markov (1.5 h)
- Processus gaussiens (1.5 h)
- Modèles de mélanges (1.5 h)
- Modèles de Markov cachés (1.5 h)
- Filtre de Kalman (1.5 h)
- Echantillonnage (1.5 h)
- Inférence variationnelle (1.5 h)
TD:
- Processus de Poisson et de Markov (1.5 h)
- Modèles de Markov cachés (1.5 h)
- Filtre de Kalman (1.5 h)
- Echantillonnage (1.5 h)
TP:
- Processus gaussiens (3.0 h)
- Modèles de mélange (3.0 h)
- Filtre de Kalman et particul. (3.0 h)
- Echantillonnage (3.0 h)